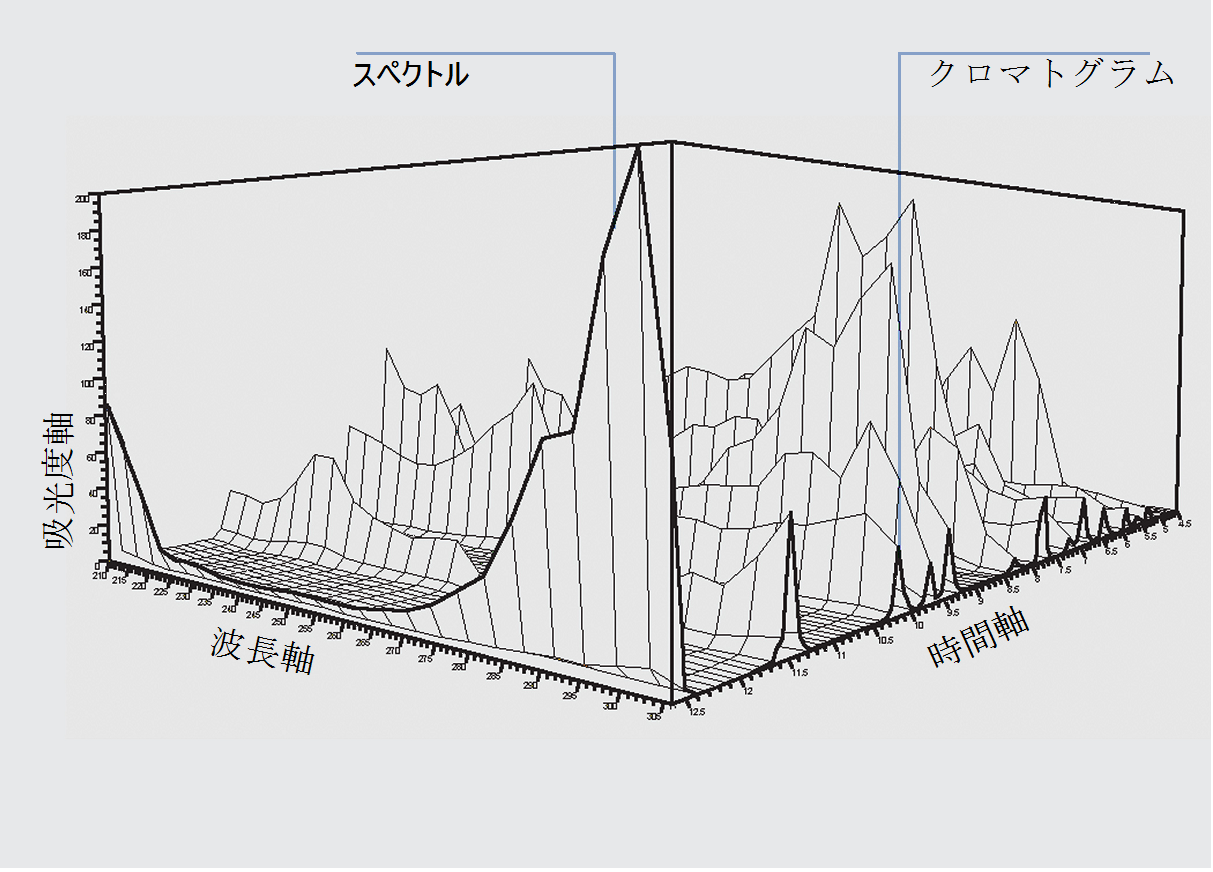
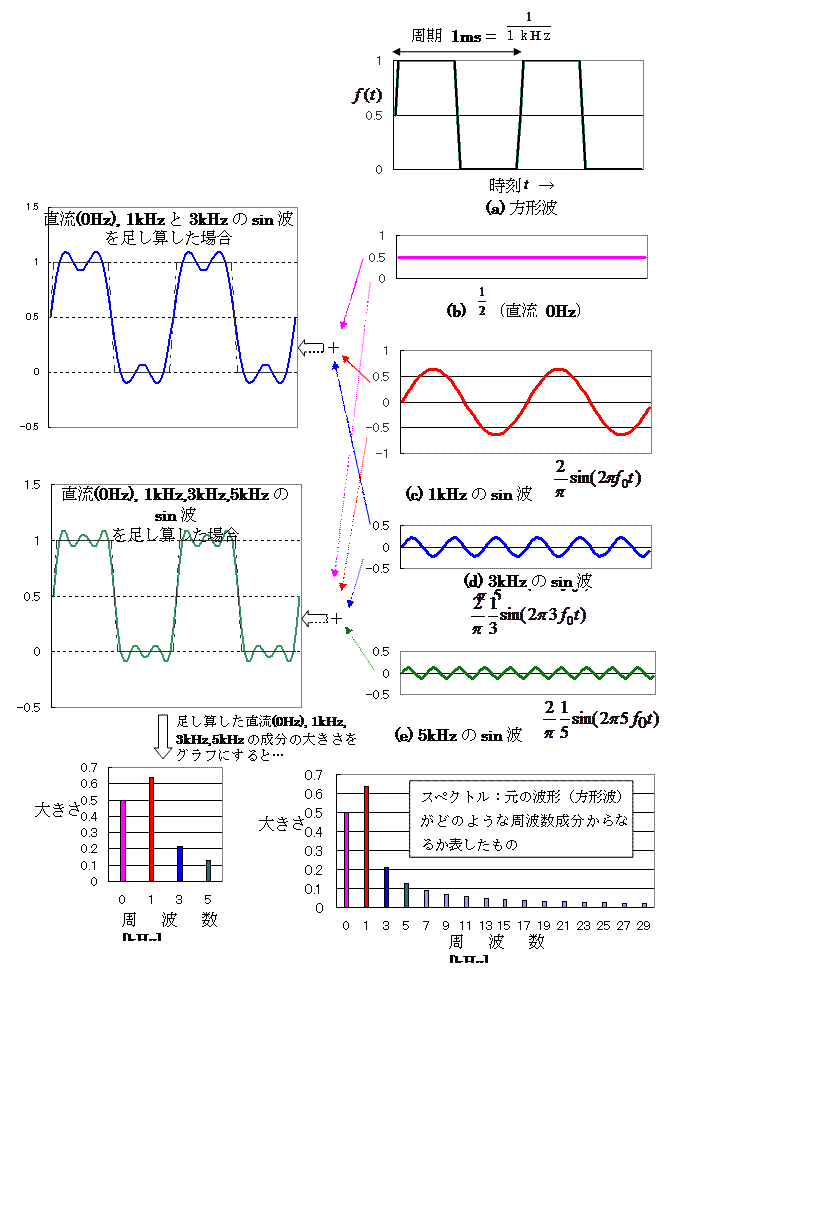
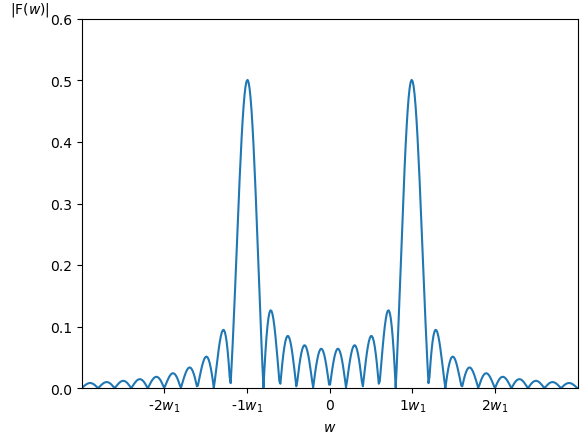
周波数スペクトルを周波数(角振動数)の関数とみなしたとき、これをスペクトル関数とよぶ。また、時間的変動を周波数でなく、特性時間などの周波数以外の変数について分解した場合も、一般にスペクトル関数とよぶ。
スペクトル関数がわかれば、時間的に変化する元の変数を書き表すことが出来る。例えば、周波数スペクトル関数をとすると、元の変数は
ただしCはの定義によって定まる定数で、としたり、としたりする。
緩和が本質的であるような現象では、緩和スペクトルをとすると
である。スペクトル関数はかなり一般的な言葉で、スペクトルとほぼ同意語である。