地球楕円体

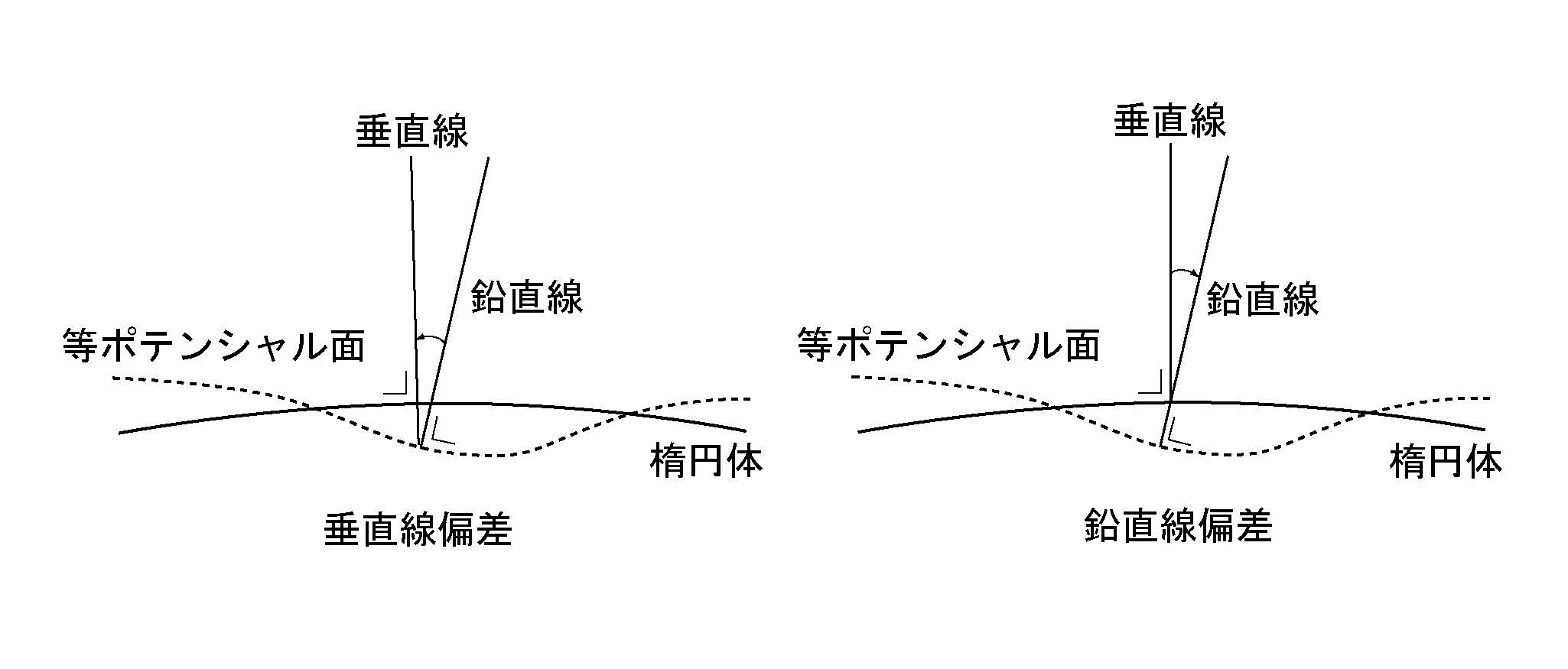
地球楕円体（ちきゅうだえんたい、英: Earth ellipsoid）とは、測地学において地球のジオイド（平均海面）の形に近似した回転楕円体（扁球）を指す。その中心は地球の重心に、短軸は自転軸に一致させる。

現在の測地系は陸域ではGRS80地球楕円体を採用する場合が多い。測地測量の基準として用いる地球楕円体は「準拠楕円体」とも呼ぶ。

地球楕円体の面に沿った経線弧（南北方向の測地線）を子午線弧と呼ぶ。歴史的には、子午線弧の研究を通じて、地球が球体を成していることが示され、また地球楕円体は、赤道半径に比べて極半径の小さい扁球なのか、それとも長球なのかを決める研究が行われた。

GRS80楕円体

GRS80は準拠楕円体のひとつで、現在世界の測地系で最も広く使われている。GRS80楕円体の長半径（赤道半径）a 及び扁平率 f は、

$a=6\ 378\ 137{\rm {m}}\,$
$f={\frac {1}{298.257\ 222\ 101}}$

肉眼だと、扁平率約1/300の回転楕円体と真球とを区別できない。ただし、現実の地球上ではこの歪み（赤道半径と極半径の差）が約21kmに達する。

WGS84楕円体

海域の測地系はWGS84を用いることが多い。WGS84楕円体の扁平率 f は、GRS80楕円体とはごく僅か異なっている。

$f={\frac {1}{298.257\ 223\ 563}}$

この差異は、地球の短半径（極半径）にすると、約0.105mmだけ異なるものであり、実用上は全く問題とはならない差異である。

WGS84楕円体は元々はGRS80を基にしたものではあるが、数値の導出過程が異なっている。すなわち、扁平率を決定するに当たって、正規化された2次の帯調和重力係数から計算により導出した際に、基となるGRS80の力学的形状係数J2の有効数字を8桁で打ち切ったために、僅かな差が発生したのである。

日本

日本における準拠楕円体は、2002年までベッセルにより算出された値（ベッセル楕円体）を採用していた（「日本測地系」と呼称）が、海図の国際利用や精密な位置情報にもとづくGISデータの整備の障害になりつつあったため、2002年4月1日から世界測地系としてGRS80地球楕円体が準拠楕円体として採用された。この新しい準拠楕円体の長半径（赤道半径）a 及び扁平率 f の値は、測量法施行令第3条により定義され、GRS80楕円体の値である。